Retrieve and wrangle data
library(dplyr)
library(tidyr)
library(purrr)
library(tibble)
load_fb_advanced_match_stats <- function(country, gender, tier, stat_type, team_or_player, season_end_year = NA) {
url <- sprintf(
'https://github.com/JaseZiv/worldfootballR_data/releases/download/fb_advanced_match_stats/%s_%s_%s_%s_%s_advanced_match_stats.rds',
country,
gender,
tier,
stat_type,
team_or_player
)
readRDS(url(url))
}
possibly_load_fb_advanced_match_stats <- purrr::possibly(
load_fb_advanced_match_stats,
otherwise = tibble::tibble(),
quiet = TRUE
)
params <- tidyr::expand_grid(
country = c('ENG', 'ESP', 'FRA', 'GER', 'ITA'),
gender = 'M',
tier = '1st',
stat_type = 'summary',
team_or_player = 'player'
) |>
as.list()
raw_player_match_stats <- purrr::pmap_dfr(
params,
possibly_load_fb_advanced_match_stats
) |>
dplyr::filter(
## stop at 2022/23 season
Season_End_Year < 2024L,
## don't include keepers
!grepl('GK', Pos)
)
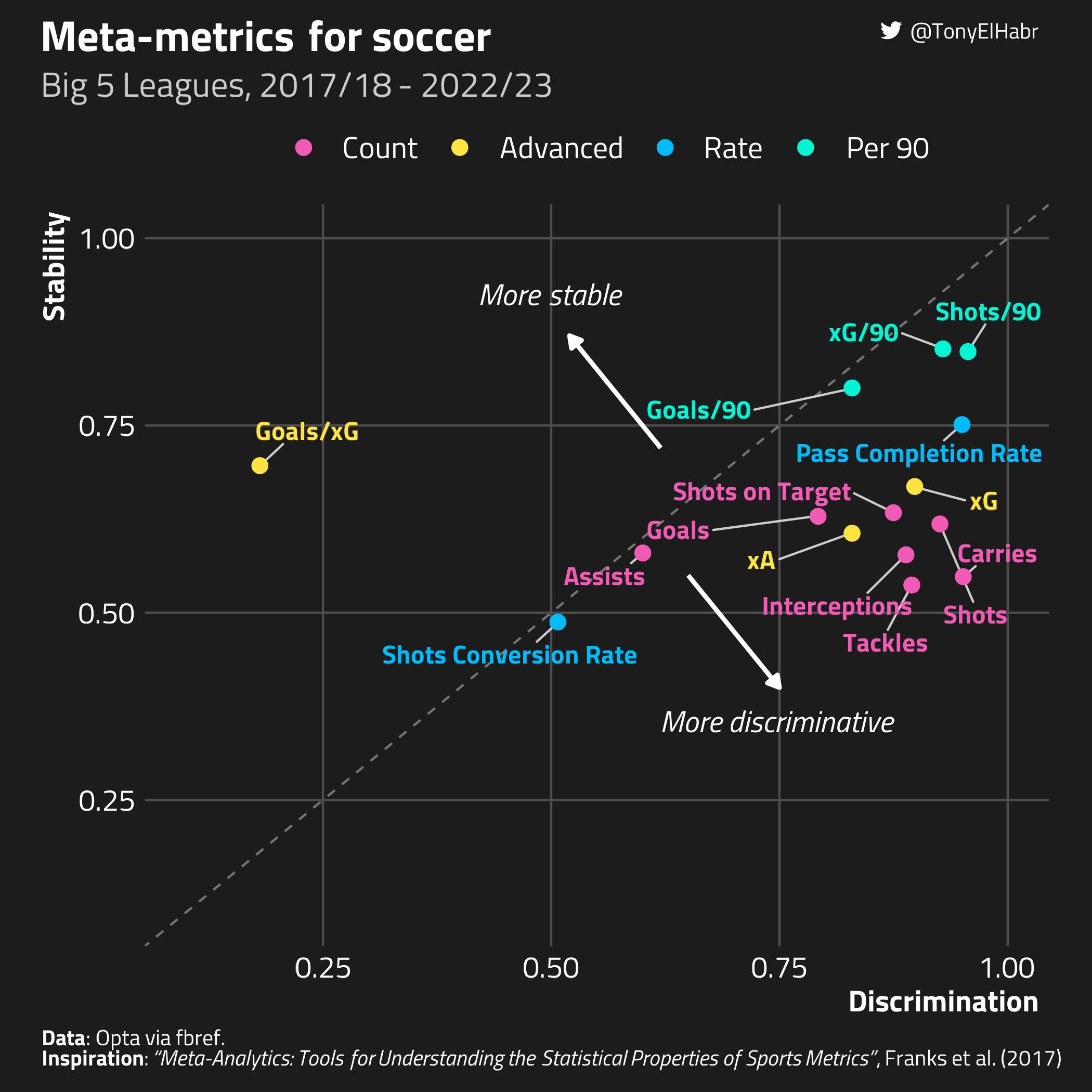
ALL_METRICS <- c(
'goals' = 'Goals',
'assists' = 'Assists',
'shots' = 'Shots',
'shots_on_target' = 'Shots on Target',
'tackles' = 'Tackles',
'interceptions' = 'Interceptions',
'xg' = 'xG',
'xa' = 'xA',
'goals_xg_ratio' = 'Goals/xG',
'carries' = 'Carries',
'shot_conversion_rate' = 'Shots Conversion Rate',
'pass_completion_rate' = 'Pass Completion Rate',
'goals_p90' = 'Goals/90',
'shots_p90' = 'Shots/90',
'xg_p90' = 'xG/90'
)
safe_divide <- function(num, den) {
ifelse(
den == 0 | is.na(den),
NA_real_,
dplyr::coalesce(num / den, 0)
)
}
coalesce_fraction <- purrr::compose(
\(num, den) safe_divide(num, den),
\(x) ifelse(x > 1, 1, x),
\(x) ifelse(x < 0, 0, x),
.dir = 'forward'
)
add_rate_and_p90_metric_columns <- function(df) {
df |>
dplyr::mutate(
## Mark Noble with the epic 1 goal on 0 shots https://fbref.com/en/matches/b56fd899/Watford-West-Ham-United-December-28-2021-Premier-League
shot_conversion_rate = coalesce_fraction(goals, shots),
pass_completion_rate = coalesce_fraction(passes_completed, passes_attempted),
goals_xg_ratio = safe_divide(goals, xg)
) |>
dplyr::mutate(
dplyr::across(
c(goals, shots, xg),
list(
p90 = \(.x) 90 * .x / minutes_played
)
)
)
}
summarize_all_metric_columns <- function(df, ...) {
matches_played <- df |>
dplyr::group_by(league, season, team, player) |>
dplyr::filter(minutes_played > 0L) |>
dplyr::summarize(
matches_played = dplyr::n_distinct(match_id)
) |>
dplyr::ungroup()
df |>
dplyr::group_by(..., league, season, team, player) |>
dplyr::summarize(
dplyr::across(
c(minutes_played:dplyr::last_col()),
sum
)
) |>
dplyr::ungroup() |>
add_rate_and_p90_metric_columns() |>
dplyr::inner_join(
matches_played,
by = dplyr::join_by(league, season, team, player)
) |>
dplyr::relocate(
matches_played,
.before = minutes_played
)
}
player_match_stats <- raw_player_match_stats |>
dplyr::transmute(
league = sprintf('%s-%s-%s', Country, Gender, Tier),
season = sprintf('%s/%s', Season_End_Year - 1, substr(Season_End_Year, 3, 4)),
date = Match_Date,
match_id = basename(dirname(MatchURL)),
team = Team,
player = Player,
minutes_played = Min,
goals = Gls, ## includes pks
assists = Ast,
shots = Sh, ## does not include pk attempts
shots_on_target = SoT,
tackles = Tkl,
interceptions = Int,
passes_completed = Cmp_Passes,
passes_attempted = Att_Passes,
carries = Carries_Carries,
xg = xG_Expected,
xa = xAG_Expected
) |>
add_rate_and_p90_metric_columns()
player_season_stats <- summarize_all_metric_columns(player_match_stats)
## Franks et al. used 250 min played for the NBA
## https://github.com/afranks86/meta-analytics/blob/1871d24762184afa69f29a2b5b348431e70b9b2b/basketballReliability.R#L60
MIN_MINUTES_PLAYED <- 270
eligible_player_season_stats <- player_season_stats |>
dplyr::filter(minutes_played >= MIN_MINUTES_PLAYED)
eligible_player_match_stats <- player_match_stats |>
dplyr::semi_join(
eligible_player_season_stats,
by = dplyr::join_by(league, season, team, player)
) |>
dplyr::arrange(league, season, team, player)
## drop players with 0s for any given metric across any season?
## looks like they only did that for testing a 1-season evaluation:
## https://github.com/afranks86/meta-analytics/blob/1871d24762184afa69f29a2b5b348431e70b9b2b/basketballReliability.R#L25
# eligible_player_season_stats |>
# pivot_metric_columns() |>
# group_by(league, team, player, metric) |>
# summarize(has_any_zero = any(value == 0)) |>
# ungroup() |>
# filter(has_any_zero)